前言
最近在工作中又碰到了DH(Diffie-Hellman)算法,鉴于之前对该算法理解地支离破碎,因此在博文中总结归纳下。
原理
DH算法用于在不安全的公共通道中协商密钥,安全性体现在:在有限域上计算离散代数非常困难。上两位大牛Whitfield Diffie 和 Martin Hellman的照片:

算法描述:
假定Alice和Bob期望在一个不安全的网络中协商一个共同的密钥,那么进行如下步骤:
- 两人先说好大素数(质数)p和它的原始根g。
- Alice随机产生一个数a,并计算
A = p^a mod g, 发送给Bob。 - Bob随机产生一个数b,并计算B= pb mod g,发送给Alice。
此时, Alice手握Bob发过来的B,结合自己产生的a开始这样计算:
B^a mod p = (p^b mod g)^a mod p = p^ab mod g。
Bob也拿到了Alice发来的A,同时结合自己的b,也开始计算:
B^a mod p = (p^b mod g)^a mod p = p^ab mod g。
这样Alice和Bob都得到了相同的密钥。
DH的安全缺陷
DH不仅支持两点密钥交互,也可以支持多点密钥交互。但是DH算法本身存在安全性缺陷,即没有对交互双方进行身份验证,容易遭受中间人攻击。攻击思路具体如下:
- Alice本来想发送A给Bob,被EVE截胡,EVE自己选择一个私有数c,计算出
C = p^c mod g,发送给Bob。 - Bob本来想发送B给Alice,也被EVE截胡,EVE再把
C = p^c mod g发送给Alice。 - 此时,Alice和EVE计算出共同的密钥
K1 = p^ac mod g,Bob和EVE计算出共同的密钥K2 = p^bc mod g。 - Alice和Bob都以为是和对方协商好了共享密钥,于是开始发送数据,Alice用K1加密数据后发送给Bob,又被该死的EVE截胡,EVE用K1解密,不仅可以看到Alice想对Bob发送的信息,还可以修改,然后再用K2加密该篡改之后的信息,发给蒙在鼓里的Bob。Bob当然可以用K2解开,但是已经被EVE窥探甚至修改。
因此必须引入身份验证以防范此类攻击,利用RSA数字签名即可达到此目的。
DH在TLS中的应用
DH算法作为一种密钥协商机制,可以用于TLS协议当中。
如果在DH交互过程中Alice和Bob始终使用相同的私钥,就会导致后续产生的共享密钥是一样的,如果有嗅探者截获通信双方的所有数据,由于都是同一个密钥加密所得,一旦被破解,后续的通信将全部暴露。
为了保证安全性,必须引入前向保密,即Forward Secrecy。其基本实现思路就是在Alice和Bob在选择各自的私钥是引入随机性,也印证了那句话:要用发展的眼光看问题,不能一成不变。
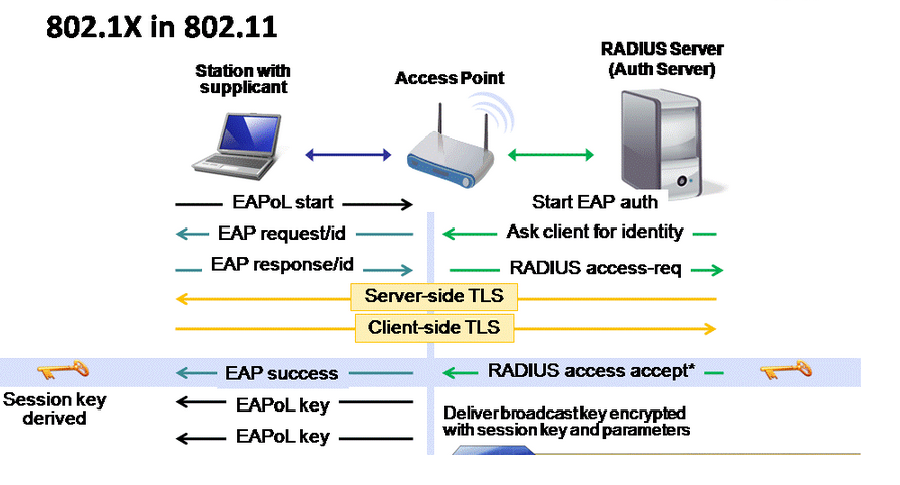
事实上FS在诸多加密协议中应用广泛,比如IKEv2和802.11i密钥分发中的4-way握手,无一不引入此方法。
那么问题来了,TLS中哪一个才是最安全的cipher呢?就目前而言,最安全的三个候选者如下:
TLS_ECDHE_RSA_WITH_AES_256_CBC_SHA384_P521TLS_ECDHE_RSA_WITH_AES_256_CBC_SHA384_P384TLS_ECDHE_RSA_WITH_AES_256_CBC_SHA384_P256